Comparing approaches to experimental analysis

Clear and unbiased analysis methods are critical to understanding the experiments that businesses run in-market on real users. Traditionally, such online experimentation has relied on Null-Hypothesis Significance Testing (NHST) to choose winning variants. However, more recent work has highlighted shortcomings of this approach. In this post, we review the current trend of moving towards different approaches to experiment analysis.

Problems with the traditional approach

The field of online experimentation¹ has grown immensely over the past decade, by applying methods from scientific research (e.g. clinical trials in medicine) to the digital domain (e.g. website optimisation with A/B testing). If you use a product like Optimizely or Adobe Target, you are relying on these methods, whether you realise it or not.

Often in business settings, the goal is to pick the best performing variant from a set of options (e.g. choosing a variant of a webpage that yields the highest conversion rate). These decisions have largely been driven by using an approach known as Null-Hypothesis Significance Testing (NHST) (e.g. t-tests). The goal of a NHST experiment is to determine whether or not we can reject the null hypothesis (e.g. concluding that one variant has a better conversion rate than the other).

With NHST, a null hypothesis (e.g. the two variants of the webpage will yield the same conversion rate) and an alternate hypothesis (e.g. the two variants of the webpage will yield different conversion rates) are defined. The goal of a NHST experiment is to determine whether or not we can reject the null hypothesis (thereby accepting the alternate hypothesis). Before the experiment is run, the sample size needs to be determined, to ensure that the experiment will have enough power (i.e. will detect the difference between variants if there is any). To calculate the required sample size, the experimenter must make some assumptions about the expected effect size (e.g. how different the conversion rates will be between webpage variants). The experiment needs to adhere to this pre-calculated sample size to be valid.

Once the experiment has been run, then conclusions about it are based on the calculations of the p-value, which is the probability of seeing data as extreme as the experiment’s results, given the experimental conditions. Conventionally, p-values greater than 0.05 are taken to mean that the null hypothesis cannot be rejected (e.g. that there is no difference between webpage variants) and p-values less than 0.05 are taken to mean that the null hypothesis can be rejected (e.g. that there is a difference between webpage variants).

The NHST approach has its benefits: straightforward formulas, clear decision thresholds, and almost a century of use across wide-ranging disciplines. For example, it is used by Adobe Target² for A/B testing. However, NHST also has its drawbacks:

• Although it has clear rules on how to run experiments, these can be impractical to follow³ in real-world situations. For example, there is a requirement to commit to the sample size calculated before the experiment started; you cannot stop the experiment early or continue running it for longer if you’re not satisfied with the results.
• The abundance of data means that it is easy to get spurious results from multiple comparisons⁴. For example, imagine running tests comparing 100 quantities, where the null hypothesis for all of them is actually true. We would expect about 5 of the tests to show significance at the p < 0.05 level, just due to chance.
• Typically, experimenters have the ability to peek at results before the experiment ends, and if these results are used in criteria for stopping the experiment, these will introduce a bias in the results⁵. If you peek at the results frequently, you increase the likelihood of observing p < 0.05 (and therefore reject the null hypothesis) due to chance (i.e. there is no real effect). If you also stop experiments as soon as you observe p < 0.05, then it’s likely that some of your experiments will appear to find an effect when there is none.
• Confidence intervals are unintuitive and difficult to interpret correctly⁶. For example, there is a strong temptation to interpret a 95% confidence interval as the region where we are 95% confident that the true value lies within. This is incorrect. The correct interpretation is that if we repeated the experiment many times and calculated the confidence interval each time, then 95% of these confidence intervals would contain the true value. Also, confidence intervals are determined by p-values, which can change from one experiment to the next, depending on the stopping rule ⁷.
• The reliance on p-values encourages black-and-white thinking around an arbitrary threshold, which oversimplifies results. There is nothing special about the p = 0.05 level, and results that have p = 0.049 and p = 0.051 aren’t that different, even though they are treated as such. Indeed, there have been calls to abandon statistical significance⁸ altogether.

The idea that the traditional NHST approach is not well suited to modern applications is perhaps unsurprising. They were developed by Fisher⁹ for agricultural experiments on fertilisers, and were aimed at extracting the maximum amount of information from a minimal amount of data. For this application, the fixed number of seeds that can be planted in a plot effectively commits you to a fixed sample size. Also, you can’t peek at results because they only arrive at the end of the experiment (after the plants have matured).

These issues have led to some experimenters to adopt approaches⁷ that focus less on hypothesis testing, and more on effect size measurement. This is because typical experiments in modern settings are more concerned with the latter and less concerned with the former.

Sequential testing: a more flexible approach

One of the shortcomings of the traditional NHST approach is that it requires experimenters to estimate the effect size before the experiment, which is then used to commit to an experiment sample size. Once the experiment begins, the sample size cannot be changed.

An alternative approach that avoids this problem is sequential testing¹⁰, which was developed by Wald as a way to ‘A/B test’ munitions for the US navy¹¹. In this kind of application, the goal is to only test enough to ‘pick a winner’ between candidates. In a web optimisation application, this would be like continuously monitoring the performance of multiple variants of a webpage, and deploying the best one to all users once it is established that it outperforms the other variants by a sufficient amount.

The key idea behind this approach¹² is based on false positive and false negative rates. These are how often a statistical test incorrectly rejects the null hypothesis even though it is true (i.e. it finds an effect when there really isn’t one) and how often it incorrectly fails to reject the null hypothesis even though it is false (finds no effect when there really is one). With sequential testing, the experimenter defines thresholds based on acceptable false positive and false negative rates upfront, and continuously monitors some cumulative statistic (e.g. log-likelihood ratio sum) as the experiment progresses. Once this statistic crosses one of the thresholds, a winning variant is identified and the experiment ends.

Sequential testing approaches have been adopted by Optimizely¹³, and a simplified version of this technique has also been described¹⁴.

The appeal of sequential testing is that it can potentially use smaller sample sizes than required by traditional NHST. However, such reductions in sample sizes are only realised in experiments where there is a large effect size (i.e. one variant performs much better early on, so the experiment can be ended earlier). In other cases, it may end up requiring a larger sample size. In typical website optimisation experiments, effect sizes tend to be small, so it isn’t clear that they would see the benefits of sequential testing.

Sequential testing also disregards effect size and uncertainty, which may be of interest in some experiments that have a wider scope beyond the requirement to ‘pick a winner’.

Profit-maximising tests: the cost of experimentation

A more recent approach¹⁵,¹⁶ is to predict the costs and benefits of running the experiment as a function of sample size, and then commit to a sample size that maximises the net benefit.

This approach predicts the expected lift (from choosing the best performing variant) as a function of experiment duration. This lift is time-discounted to account for the cost of running a longer experiment (i.e. the longer you run the experiment for, the longer you have to wait before deploying the winning variant to reap the rewards). By simulating the time-discounted expected lift for different sample sizes, it’s possible to find the sample size that best balances the tradeoff between running an experiment longer (to get an accurate result) but not too long (to extract value from the result).

An advantage of this approach is that the optimium sample size can be found for a specific application, and can lead to smaller sample sizes than recommended by traditional NHST. This is because the costs of large sample sizes are considered explicitly, and specific applications may have more permissive decision thresholds (rather than the conventional p=0.05 threshold, which may be too conservative).

However, a disadvantage is that it still requires an upfront commitment to the sample size before the experiment begins. This decision is based on some assumption about the sample’s true variance, which is difficult to know in advance.

Bayesian effect size estimation: answering the right question

Statistical approaches can generally be described as frequentist or Bayesian. Frequentist approaches (e.g. traditional NHST) answer the question: ‘What is the likelihood of seeing this data, given a hypothesis?’. In contrast, Bayesian approaches answer a different question: ‘What is the probability of this hypothesis being true, given that we have seen this data?’. The latter question is a closer fit to what typical experiments are trying to answer. For example, the question: “What is the probability that this webpage variant’s true conversion rate is 5%, given the data we have observed?” is more relevant than “What is the likelihood of observing the data we have observed, assuming the conversion rate is 5%?”. These methods are already being used at companies like VWO¹⁷.

Bayesian approaches provide probability distributions of possible effect sizes (called posteriors), making uncertainty estimates more intuitive. Instead of relying on confidence intervals to quantify uncertainty, a Bayesian credibility interval¹⁸ is simply the range containing a particular percentage of probable values (e.g. the 95% credibility interval is the central portion of the probability distribution that contains 95% of the effect size values). This allows more intuitive statements to be made (e.g. ’there is a 95% probability that the true value lies within this range’). One type of credibility interval is the High Density Interval (HDI), which further requires that all points within the interval have a higher probability density than points outside the interval, as shown below.

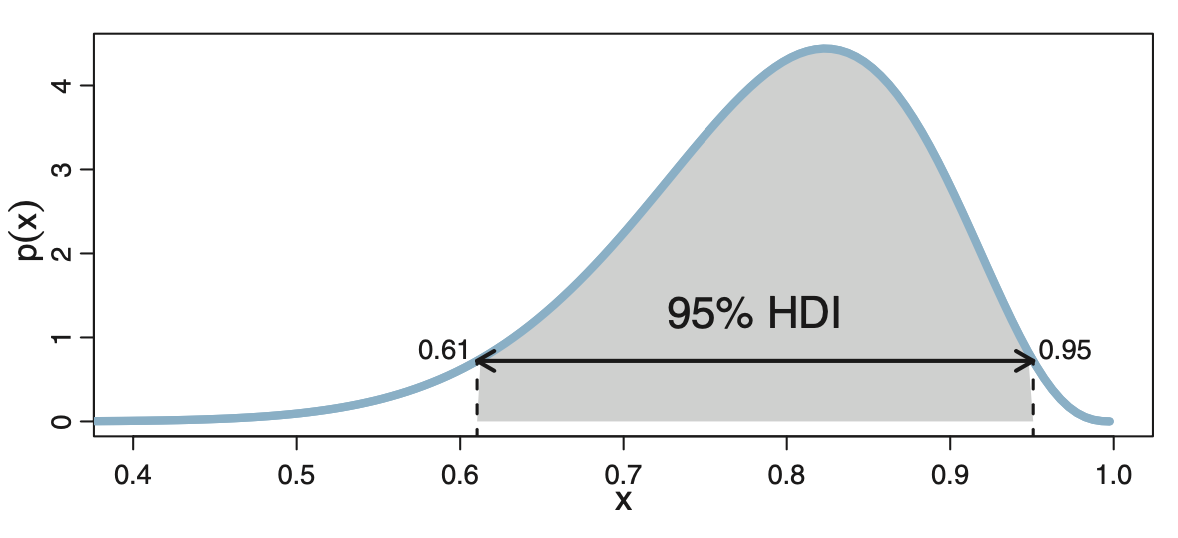
The focus on effect size estimation⁷, rather than hypothesis testing, gives richer information about how strong the causal effects of our interventions are. This is important if are interested in more than just the ability to ‘pick a winner’.

However, clear decisions can still be made with these approaches. Instead of requiring the effect size as input to define a fixed sample size (as in traditional NHST), one Bayesian approach requires us to define a Region Of Practical Equivalence (ROPE) around a null value. This is defined by the set of values that are practically equivalent the null value for a given application. For example, if we were comparing the conversion rates between webpage variants, the null value for the difference in conversion rates would be zero. We may decide that it’s not worth the cost of switching to a variant (i.e. they are practically equivalent) if the difference in conversion rates is less than 0.1%. The ROPE in this example would cover the range from -0.1% to 0.1%.

The posterior distributions produced by Bayesian effect size estimation allow experimenters to calculate the HDI, and compare its position relative to the ROPE. If the HDI overlaps the ROPE, then the results are practically equivalent (e.g. we would accept the null hypothesis that the webpage variants are practically equivalent). The advantage of this approach is that it’s easier to define a ROPE around the null value ahead of an experiment than it is to predict the effect size (which would be required for traditional NHST).

Traditional NHST can be done incorrectly by stopping the experiment too early, or by continuing to run the experiment after the sample size has been reached (e.g. continuing to experiment until a postive result is reached). The biased results that this kind of ‘optional stopping’ introduces is a problem for all approaches, including Bayesian ones.

This can be mitigated by ensuring that the criteria for stopping the experiment are not based on the experiment results, but on a pre-defined critical precision ¹⁹. With this approach, the risk of biasing the results is negligible. For example, we could commit to running the experiment until the width of the HDI reaches 80% the width of the ROPE.

For binary outcomes (which are common in A/B testing), the relevant probability density functions can be approximated by using the beta distribution²⁰,²¹. The only two quantities required for these calculations are the number of ‘successes’ (e.g. number of conversions) and the total number of trials (e.g. number of sessions where a webpage variant was displayed). The simplicity of this approach has led to it being described as “so easy it feels like cheating”²².

A disadvantage of this approach is that if we cannot rely on simple analytical solutions like the beta distribution, then the calculations of the probability density functions require more advanced techniques like Markov Chain Monte Carlo (MCMC) simulations, which can be time-consuming.

What we do at Ambiata

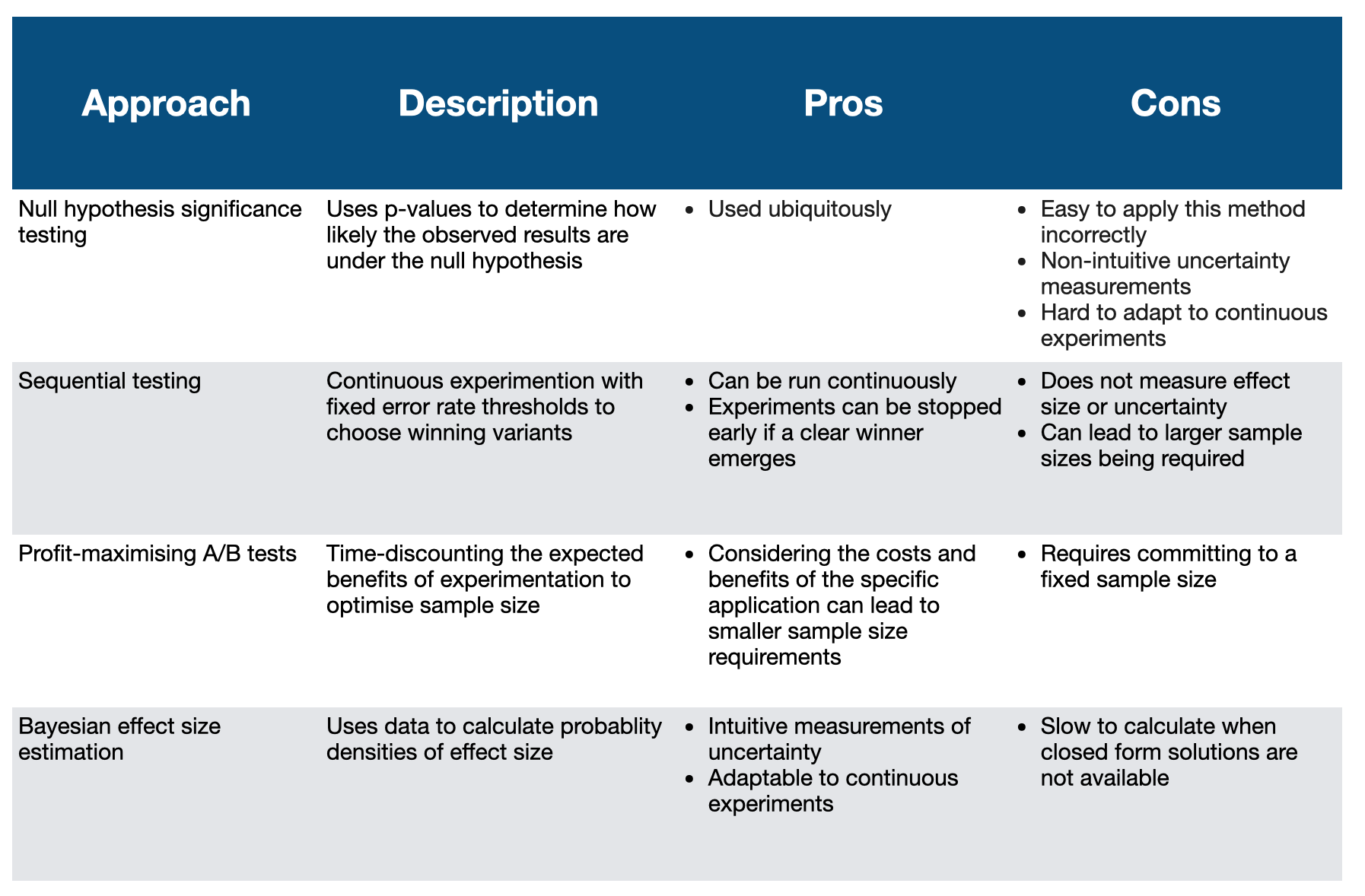
This post has described a number of approaches listed in the table below:

We would like to follow an approach that meets the following requirements:

• It must be accurate
• It needs to quantify uncertainty
• It must be possible to make it intuitive to stakeholders
• It should be easy to compute

We find that Bayesian effect size estimation meets these requirements. It is accurate (traditional NHST relies on normal approximations because it was developed before modern computing). With its emphasis on probability distributions, it provides intuitive descriptions of uncertainty. These are easier to communicate to stakeholders than confidence intervals. It is also easy to compute in situations where closed-form solutions exist, and there are extensive libraries²³ available for situations where they don’t.

Note that effect size estimation as described here assumes that all users respond to a treatment in the same way. For example, given treatment A and treatment B, we decide whether A or B performs the best on average, for everyone. The winning treatment would be deployed to all users, while the other treatment would be discarded. However, it may turn out that treatment A is the best for certain users, while treatment B is the best for another set of users. In this case, we might want to deploy both treatments, but have some way to choose the best treatment for each user. This is the concept behind personalised medicine, where the treatment prescribed to a patient is customised to their individual characteristics, as opposed to being chosen based on the average effect across a wider population. One solution to this problem is called a “contextual bandit”, which we will describe in another post.