What is a contextual bandit? How does it enable continuous intelligence and real-time decision-making? In this post, we will answer these questions and explain why these algorithms are important.
The Problem
Imagine you are tasked with building a machine that can receive a stream of users and automatically choose the best option for each user in real-time. The only thing you know is that you will need to keep making this decision for more users. You don’t know which option is best for each user, you have to try each one to find out. Furthermore, the outcomes are probabilistic - a bad option can appear to perform well by chance, and vice versa. How do you find the best option for each user, as quickly as possible?
Computer scientists have come up bandit algorithms to solve this kind of problem, where a series of decisions must be made sequentially under uncertainty. We can think about this intuitively like a game, which consists of a sequence of independent rounds. In each round, the machine has to choose from a set of available options. Each option may lead to a different reward, and there is an element of chance as to how good the reward is. One option may tend to be better than the other, but not always.
The machine only sees the reward of the chosen option, and uses the result of past decisions to inform the next decision. The only way to learn the reward distribution of each option is to try it. How does the agent play this game to maximise the reward collected over all rounds?
A real-life example of this game would be if you had to choose a restaurant to dine at every week, where the reward is how much you enjoy the meal. Do you stick with your current favourite, which is a safe and reliable choice? Or do you take a risk and try something new, which could be end up being much better (or worse)? Another example would be waiting for a late-running bus for a short trip. Are you better off walking (which takes longer but you’re more certain about), or waiting (which is faster, if the bus arrives)?
To explain how we achieve this at scale, we start with two concepts: experimentation, and machine learning.
Experimentation
Experimentation here refers to randomised controlled trials (RCTs), which are widely accepted as the gold standard for drawing causal conclusions about various treatments (e.g. clinical trials in medicine). While it is possible to measure effects of interventions in observational studies, any links between treatment effect cannot be simply consdered as causal, because they are subject to various biases (e.g. selection bias). For example, simply observing that private school students have higher incomes than public school students later in life does not necessarily mean that private school attendance causes higher incomes, it could be that students with wealthy families tend to go to private schools, and it is actually their background that leads to higher incomes.
Specifically, the form of experimentation we refer to here is called online experimentation, where the experiment is continously updated as more data becomes available. Digital applications tend to have the continuous data streams that fit this description, as opposed to clinical trials, which tend to be done in batches.
The key idea behind experimentation is shown in the diagram below, where a stream of users are randomly assigned to various options. This allows us to measure the resulting performance of each option and be confident that any difference in performance can be attributed to the options, and not some other confounding effect.
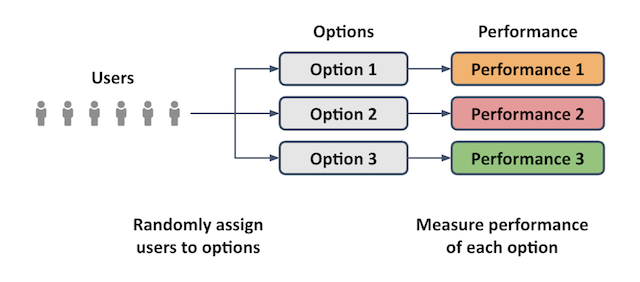
In our restaurant analogy, this would be like trying all the available restaurants by choosing a random one each time. You would get a good idea of the quality of each restaurant, but you might also have to get through some poor quality visits to find out.
Machine Learning
Machine learning here refers specifically to supervised learning, where datasets consisting of feature variables and a target variable are used to train a model. The traditional applications of supervised learning are classification and regression - the task is to predict the value of an unknown target variable based on the associated features. For example, companies may want to predict how likely a customer will churn (target variable), based their demographics, product holdings, and transaction history (features). Such a model does not tell you what you should do to that customer to achieve the best outcome, it only tells you what is likely to happen absent any intervention.
Supervised learning is illustrated in the figure below, where each user has a row of features and a binary target variable (e.g. whether or not they clicked the link on a website). The resulting model can then be used to predict the target variables of a new set of users, based on their features.
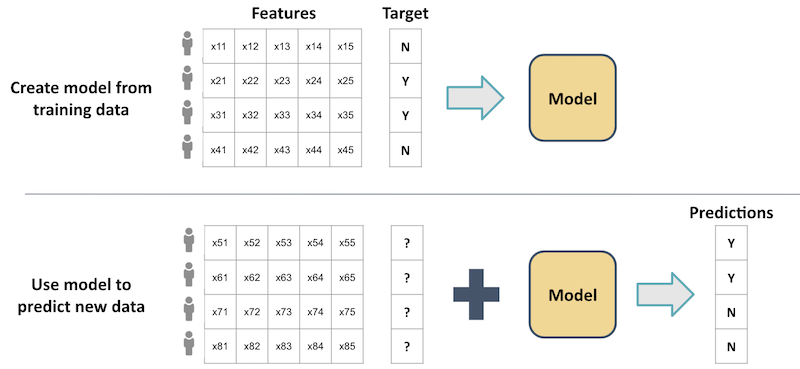
In our restaurant analogy, this would be like using what you already know to pick your favourite restaurant every time. This would be a safe choice, but if there are better options available, you would never discover them.
Contextual Bandits
Now, let’s consider how an online, decision-making agent would operate as a contextual bandit, as shown schematically in the figure below.
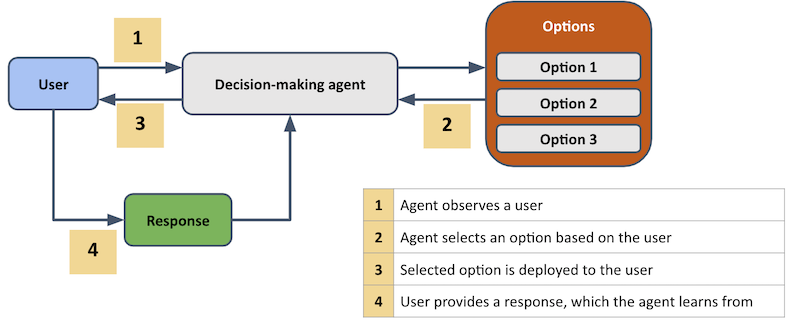
Here, there are four steps that are performed iteratively over a sequence of users.
- Firstly, the agent observes a user, as well as any relevant context that is available.
- The agent then assigns an option to this user, based on their context and the agent’s internal model at that point in time.
- The chosen option is then deployed to the user.
- The user then responds to it in some way, and the agent records this response. The agent now has information (i.e. the user’s response, context and the assigned option) to learn what it should do next time it sees a similar user.
An example of this is website optimisation, where a sequence of users arrive on a website, and an agent has to decide which variant of the page to display to the user, based on their context. Once the chosen variant is displayed, the resulting user response (e.g. clickthrough, conversion, etc.) is logged by the agent and used to update its internal model.
Experimentation + Machine Learning
A useful way to think about the decision-making agent is to break it down into its component experimentation and machine learning parts, as shown below.
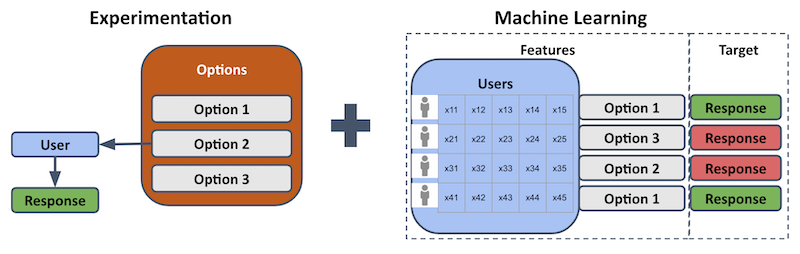
The description here refers to the contextual bandit approach (other approaches, such as uplift modeling, also exist). Contextual bandits use experimentation, because options are (probabilistically) assigned to users, and the resulting user response is recorded as a performance measure. Contextual bandits also use machine learning, because the user contexts and assigned options are used as features in supervised learning. The corresponding target variable is the user response, given an assigned option and user context. This allows us to train models to predict what the response will be to an option, given their user context.
However, unlike traditional supervised learning, the contextual bandit learns iteratively by interacting with the user population and observing the resulting reponse. Unlike traditional experimentation, the user context allows us to predict the best option for each user, not just the best option overall. If the user context is irrelevant (e.g. all users are identical), then the expected response will depend only on each option’s historical performance. This simpler situation is called the multi-armed bandit setting. If the user context is important (i.e. responses to an option depend on user context), then its inclusion in the model is called the contextual bandit setting.
What makes bandit algorithms unique is that they focus on the explore-exploit tradeoff, where the need to learn about reward distributions by trying them (i.e. explore) must be balanced with the need to choose the best option as often as possible to maximise reward (i.e. exploit).
In our restaurant analogy, this would be like choosing your favourte restaurant most of the time, while sometimes trying a different one at random, just to see if it is worth switching to. If restaurant qualities change over time, then you would learn this and potentially switch to a new favourite.
It’s worth considering now how an individual user would move through this bandit algorithm system. Suppose we have already collected enough historical results (i.e. logs of user contexts, assigned options, and corresponding rewards) for each option to be able to train a reward prediction model for each option. These models take user context features to predict the reward (and its uncertainty) for each option.
There are many bandit algorithms, but at the core of each one is a method to choose an option based on the predicted rewards (and uncertainty) for each option. One such algorithm is Thompson sampling, in which the probabilty of choosing an option depends on the probability of it being the best option. If the predictions indicate that an option is likely to be the best, then it will probably (but not always) be chosen. Similarly, options that are predicted to perform worse will rarely (but sometimes) be chosen.
The Thompson sampling approach requires the probability distribution of the reward for each option and user, which might look something like this:
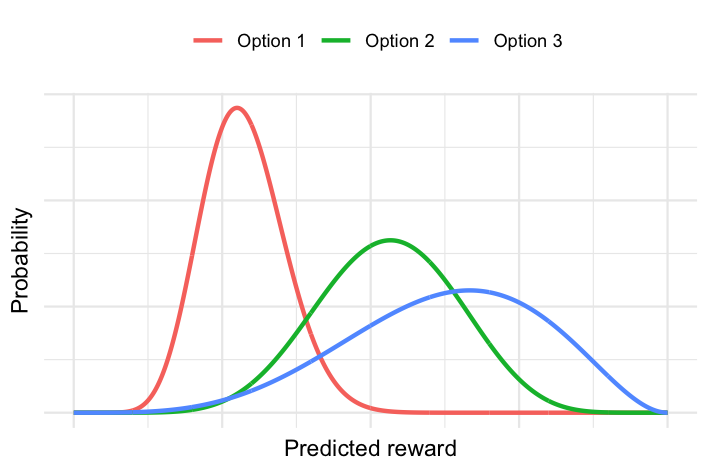
In this plot, each curve represents the reward probability distribution for a given option and user. The narrower the curve, the more certain we are about its expected reward. The further to the right the curve is, the higher the expected reward. In this example, option 1 for this user has a higher certainty at lower reward, while option 3 for this user has a larger uncertainty around a higher reward. Option 2 for this user falls somewhere in between these options.
For the current user, we sample a reward value from each of the three probability distributions. For example, it might look like the plot below:
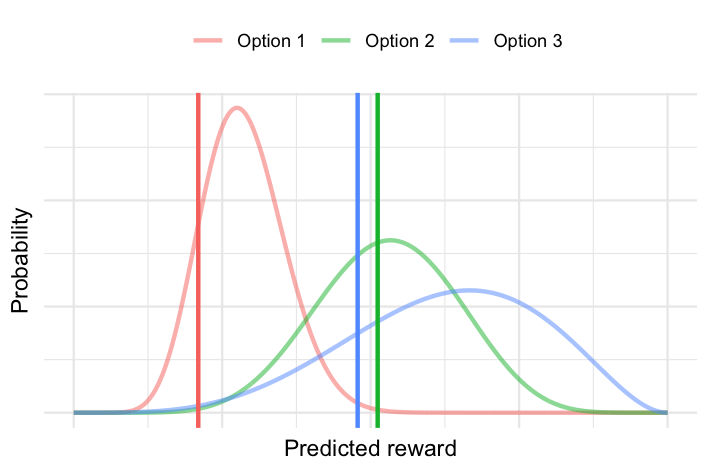
Here, the vertical lines correspond to a sample taken from each option’s reward distribution for this user. For this particular set of samples, the highest reward actually corresponds to Option 2 (even though Option’s 2 curve peaks at a lower reward than Option 3), so it would be assigned to this user.
While Thompson sampling favours options that are predicted to have high rewards (exploit), the probabalistic sampling means that it is still possible to retry an option that has previously underperformed (e.g. Option 2 in this example), especially if there is high uncertainty around it (explore). As the agent processes more users, it collects more historical results to update these probability distributions, and it develops higher certainty about the predicted reward for each user and option.
Conclusion
These ideas form the conceptual underpinnings of how contextual bandits enable continuous intelligence (i.e. real-time decision making). The key point is that bandit algorithms address the explore-exploit tradeoff inherent to sequential decision-making under uncertainty. This maps onto experimentation (to generate examples to learn from) and machine learning (enabling personalised reward predictions). Contextual bandits allow learning and optimisation to iterate simultanously, thereby creating systems that are continously intelligent.
